Brownian noise

For similar phrases, see Brown note (disambiguation).

Colors of noise
White
Pink
Red (Brownian)
Grey

In science, Brownian noise (), also known as Brown noise or red noise, is the kind of signal noise produced by Brownian motion, hence its alternative name of random walk noise. The term "Brown noise" comes not from the color, but after Robert Brown, the discoverer of Brownian motion.

1 Explanation
2 Power spectrum
3 Production
- 3.1 Sample
4 See also
5 External links
6 References

Explanation

The graphic representation of the sound signal mimics a Brownian pattern. Its spectral density is inversely proportional to f², meaning it has more energy at lower frequencies, even more so than pink noise. It decreases in power by 6 dB per octave and, when heard, has a "damped" or "soft" quality compared to white and pink noise. The sound is a low roar resembling a waterfall or heavy rainfall. See also purple noise, which is a 6 dB increase per octave.

Power spectrum

A Brownian signal is expressed mathematically as the integral of a white noise signal, 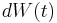$dW(t)$ , namely a Wiener process

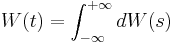
$W(t) = \int _{-\infty}^{%2B\infty} dW(s)$

White noise has a constant spectrum 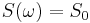$S(\omega) = S_0$ . The Fourier transform has the general property^[1]

$\mathcal{F}[f^\prime(t)](\omega) = \imath \omega \mathcal{F}[f(t)](\omega)$

Since white noise is the derivative of Brownian motion (more accurately, Brownian motion is the integral of white noise, as the derivative of a random function is not defined cf.^[2]) we conclude that the spectrum for Brownian noise is 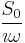$\frac{S_0}{\imath\omega}$ , therefore the power spectrum is given by

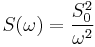
$S(\omega)= \frac{S_0^2}{\omega^2}$

Production

Brown noise can be produced by integrating white noise.^[3]^[4] That is, whereas (digital) white noise can be produced by randomly choosing each sample independently, Brown noise can be produced by adding a random offset to each sample to obtain the next one.

Sample

External links

PlayNoise, a free online white, pink, and brown noise generator, uses Javascript/HTML5.

References

^ Barnes, J.A. and Allan, D.W. (1966). "A statistical model of flicker noise". Proceedings of the IEEE 54 (2): 176– 178. and references therein
^ Gardiner, C. W.. Handbook of stochastic methods. Berlin: Springer Verlag.
^ "Integral of White noise". 2005. http://www.dsprelated.com/showmessage/46697/1.php.
^ Bourke, Paul (October 1998). "Generating noise with different power spectra laws". http://paulbourke.net/fractals/noise/.